26.: alueiden välisten ryhmien perusperiaate

Osa 1 Fake Array/Pseudo Array (osajoukon laskenta)

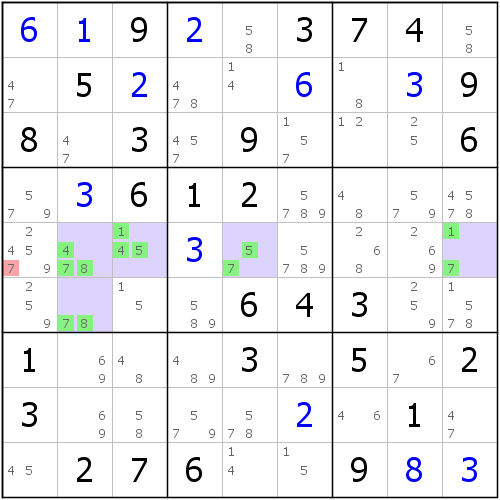
kuten kuva osoittaa. Tarkkailemme R5C2359:n ja R6C2:n viittä solua. Heillä on maaginen paikka, että vain viisi eri ehdokasta 1, 4, 5, 7 ja 8 ovat vain viisi eri ehdokasta. Tämä sattuu täyttämään taulukon määritelmän, mutta onko tämä ryhmä? sitä ei tietenkään voida määrittää suoraan. Taulukon määritelmä on, että se on määritettävä samalla alueella, ja tässä olevat viisi ruudukkoa sisältävät alueiden välisen solun, kuten R6C2 ja R5C9 Kaksi luokkaa, IT ei yhdistetä ollenkaan.

AITTELEMME TÄMÄN KYSYMYKSEN: Koska olemme hyvin samanlaisia ​​kuin Array, niin "sisäinen täyttö EI toistu" ja "sisäiset täytöt toistuvat" keskustellaksesi tilanteesta.

Huomasimme, että viisi numeroa 1, 4, 5, 7 ja 8 ON VAIN MAHDOLLINEN, ETTÄ numero 7 voidaan toistaa. Koska 7:n sijainti voidaan täyttää R6c2:ssa ja R5c9:ssä samaan aikaan, . voi olla kaksoiskappaleet. Jäljellä olevia numeroita ei kuitenkaan voida toistaa. Esimerkiksi vain 1:n sijainti näkyy R5C39:ssä, vain R5C39-vertaisissa (R5), joten näillä kahdella ruudukolla voi olla vain yksi niistä;. sama, 4-paikka Vain R5C23:ssa, Just R5C23 Peersissä (R5) ja Tong Palacessa (B4), SO 4 tässä FIVED:ssä on mahdottomumpi; 5 ja 8 analyyttistä menetelmää ovat samat (5 kaikki täyttää ehkä kaikki, 8:n täytteet voivat olla palatsin mukaisia. Joten vain digitaalisessa 7:ssä voi olla toistoa.

JOS haluat täyttää viisi numeroa 1, 4, 5, 7, 8 tähän viisiosaiseen, KUN SIINÄ, R5C9 ja R6C2 ovat 7), jäljellä olevat R5C235 kolme ruudukkoa, niitä on neljä täytetty Numerot (1, 4, 5, 8) Valinnainen. tässä Wressä, mitkä kolme numeroa valittiin ja joita emme tienneet. Joten tässä suhteessa emme voi selvitä. Mutta voimme päätellä, että vaikka se ei toistu, numero 7 on rakenteessa välttämätön. toisin sanoen näiden neljän ruudukon määrää on mahdotonta kadota levyltä. Samaan aikaan, kun se poistetaan, tässä VIISI ruudukossa on jäljellä enää neljä numeroa (1, 4, 5, 8), mutta koska niiden on oltava toistuvia, tämä ei selvästikään riitä, JOTEN SE TUOTTAA ristiriitaa., JOTKA SE JATKUU.

Sittemmin olemme tulleet siihen tulokseen: riippumatta siitä, kuinka numero täytetty sisälle, numero 7 on välttämätön, joten poistuu asema, jota neljä ehdokasta numero 7 vastaa. Siksi r5c1 <> 7.

Tätä rakennetta kutsutaan pseudotaulukoksi (tai vääräksi numeroksi, Extended Subset PrinciPle / Subset Count. Pseudo-taulukko on melko tuskallinen, ja se on erittäin kova, ja johtopäätös on niin "ruohonopeus". Niin on millään tavalla yksinkertaisempaa? TAI SANO: Kuinka tarkkailla ja käyttää nopeammin?

Osa 2 Alueiden välisen taulukon poistamisen teoria ja periaate

Pseudotaulukon analyysisuunta on yleensä sen mukainen, onko se "alueiden välinen matriisi". Jos näin on, sisäinen ei toistu;.. Jos ei, sisällä täytyy olla toistuvia numeroita. Siirry sitten toistonumeroon loppuun Pseudotaulukolla on ominaisuus Kun johdetaan periaate, se sai pisteen:... pseudo-taulukko olettaa että sisällä on toistoa, ainoa toistomäärä ei välttämättä katoa levyltä. Siksi havainnoinnin ja johtopäätöksen löytämisen yhteydessä, niin kauan kuin ainoa tarkistettava luku on, se voidaan poistaa suoraan.

Näetkö sen, SE ON RAJOITTAINEN ALUEELLINEN RAKENNE, MUTTA SISÄLLÄ EI SAA toistaa? Jotkut, kuten tämä esimerkki.

Kuten kuvasta näkyy. Huomioi R34c34 Four, Only 1, 4, 6, 8 Four Numbers INTERLY, JA TÄYTÄ NELJÄ. Nerokasta on kuitenkin se, että 1, 4, 6, 8 EI OLE toistuvia, koska kaikki numeron 1 täyttöpaikat ovat samanarvoisia, kaikki numeron 4 täyttöasennot, kaikki numeron 6 täyttökohdat, kaikki täyttökohdat 8 paikkakunnalla. Joten tämä on mahdotonta saada toistuvaa täyttöä.

Sanoimme, että jos analysoit pseudotaulukkoa, havaitaan, että se ei toistu sisällä. Tätä rakennetta kutsutaan Distributed Disjointed Subsetiksi, jota kutsutaan DDS:ksi, jota kutsutaan alueiden väliseksi taulukoksi. Joten mitä DDS-poiston pitäisi tehdä?

Sisäisten ei-toistuvien suhteiden vuoksi vyöhykkeiden välinen taulukko tulee täyttää vain näillä numeroilla, toisin sanoen nämä luvut ovat välttämättömiä. Siten esimerkiksi esimerkki täytöstä on esitetty R34C4:ssä, jäljellä olevat solut eivät voi olla 1; 6 täytteistä saattaa näkyä R4C34:ssä, joten R4:n jäljellä olevat solut eivät voi olla 6, kun taas 4 ja 8 ovat samoja. Siksi poistojen määrä on merkitty kartalle. Tietenkin tässä esimerkissä ON LISÄOHJEET, ole hyvä ja etsi se.

Osa 3 SDC ja spanned array

SDC on erityisen hankala, ja se on jaettu useisiin eri tilanteisiin keskusteltavaksi ja analysoitavaksi. Lopulta kuitenkin huomasimme, että monet "vain" olivat tyytyväisiä, kuten 1, 4 paria, 2, 6, 7 kolme ryhmää, 2, 6, 7, 2, 6, 7, 2, 6, 7 ja tämä erillinen 9, SE ON kaikki "tapahtuu". NIIN monta "JUST", ONKO SE todella aiheutettu? Katsotaanpa nyt tätä ongelmaa.

Kuten kuvassa näkyy, tämä on SDC, mutta minua ei ole jaettu oranssiin ja vihreään maalattavaksi. Koska tämä on lähempänä pseudo-taulukon analyysiä.

Käytämme pseudoarray-analyysimenetelmää, SE ON alueiden välinen seitsemän matriisi, mutta onko tämä älykäs Theled 1, 2, 3, 4 sarake (C8) ja 7, 8 9 Tong Palace (B6 ), SO se on dds. DDS:n poistoperiaatteen mukaisesti C8:n jäljellä olevien solujen ei pitäisi olla 1, 2, 3, 4; Ja B6:n jäljellä olevat solut eivät voi olla 7, 8, 9. Joten poistan ne.

SDC:N HAVAINNOINTI voi olla ongelmallisempaa, koska tarvitaan kaksi aluetta, jotta voidaan olettaa tapaus, MILLÄ MÄÄRITIT. Mutta käytä pseudo-taulukkoa, onko se hieman helpompaa?

Fusion-To-Range (SDC) ON nimi nimeltä Two-Sector Disjoint Subset tästä syystä.