Algoritmus šifrování - Bag pro systém šifrování veřejného klíče 1

Cipher - Bag algoritmus pro systém kryptografie veřejného klíče 1

Jak všichni víme, heslo veřejného klíče, ale také známé jako asymetrické heslo, je běžnější na základě následujících tří matematických problémů;

Obtíže rozkladu velkých faktorů (RSA)

Diskrétní pár extrakce (ELGAMAL)

Eliptická křivka diskrétní, aby sestra vyřešila problém (ECC)

Tento úvod se netýká výše uvedených tří typů kryptosystémů s veřejným klíčem, ale než se objeví heslo veřejného klíče, existuje algoritmus pro šifrování veřejného hesla, algoritmus batohu; algoritmus batohu je algoritmus batohu vyvinutý společností Merkle a Hellman. Může být použit pouze pro šifrování a poté bude vylepšen shamirem, aby byl dostupný pro digitální podpisy;

Bezpečnost algoritmu batohu vznikla v problému s batohem, je to úplná otázka NP, ale později zjistil, že algoritmus není bezpečný, ale protože dokazuje, jak používat NP plné problémy k veřejnému zaheslování, stojí za to učení se.

Co je algoritmus batohu: Popis: vzhledem k tomu, že předmět má jinou váhu, lze vložit několik kusů z těchto předmětů do batohu, aby se rovnal dané hmotnosti? Popis vzorce: Vzhledem k řadě hodnot M1, M2, ..., Mn a hodnotě S vypočítejte BI, splňující: s = b1 + b2m2 + ... + bnmns = b1m1 + b2m2 + ... + hodnotu bnMnbibi Může to být 0, 1,1, což znamená, že tato položka je v batohu, 0 to znamená;

Uvedu jednoduchý příklad: Tyto položky mohou vážit 1, 5, 6, 11, 14, 20, lze je sestavit do batohu s 5, 6 a 11 a batoh sestavený na 24 není možné. Obecně se zdá, že čas potřebný k vyřešení tohoto problému exponenciálně roste s rostoucím počtem položek;

Myšlenkou algoritmu batohu Merkle-Hellman je zakódovat zprávu jako řešení problému s batohem. Délka plánu se rovná počtu položek v hromadě a jasný text odpovídá hodnotě B a vypočítá se šifrovaný text a vypočítá se hodnota a následující obrázek ukazuje odstavec následujícího příkladu k šifrování. ;

Batoh ve skutečnosti existuje ve dvou různých problémech s batohem:

Lineární čas lze vyřešit;

Lineární čas není k dispozici; snadno řešitelný problém s batohem lze upravit na obtížný problém s batohem. Veřejný klíč používá obtížný problém s batohem, lze jej snadno zdokumentovat, ale není možné dešifrovat šifrovaný text, soukromá tajemství používají snadno k vyřešení problému batohu, dává jednoduchou metodu dešifrování. Lidé, kteří nevědí, zda soukromé klíče musí prolomit šifrové texty, musí vyřešit vzácný problém s batohem.

Pro snadná řešení si můžete vybrat přetížení, poté je snadné vyřešit příslušný problém s batohem. Překonaná sekvence: Je větší než její, například {1, 3, 6, 13, 27, 52} je super-sekvence a {1, 3, 4, 9, 15, 25} není.

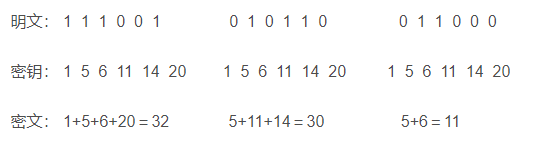
Řešení problému nadměrného přírůstku batohu lze snadno najít, vypočítat jeho celkové množství a porovnat maximální počet v sekvenci, pokud je celková hmotnost menší než toto číslo, není v batohu, pokud je celková váha je větší než toto, je v batohu, batohu Hmotnost bude odečtena, aby bylo možné zjistit další maximální číslo v pořadí, opakujte až do konce. Pokud se celková hmotnost sníží na 0, pak existuje pouze jedno řešení, jinak žádné řešení.

例如，总重量为70的一个背包，超递增序列为{2，3，6，13，27，52}；最大重量为52，小于70，所以52在背包中，70-52 = 18，下一个重量27 >18，因此，27不在背包中，在下一个13<18，13在背包中，18-13 = 5，以此类推，再下一个，3与2均在背包中，总重量减为0，表明已求出一个解，如果这个一个M-H背包加密分组，那么对应的密文70的解为110101.

Batoh s nesuperinkrementální sekvencí je obtížný, nemají žádný rychlý algoritmus. Chcete-li se rozhodnout, který z nich je v batohu, musíte postupně otestovat všechna řešení, dokud nezískáte správné řešení. Nejrychlejší algoritmus má stále potíže s inkrementací problémů v batohu, protože když se připojíte k sekvenci, řešení stačí provést další operaci.

Algoritmus batohu Merkle-Hellman tuto povahu využívá. Soukromé jádro je posloupnost vah nad přírůstky problémů s batohem. Veřejný klíč je posloupnost běžných problémů s batohem, Merkle a Hellman navrhli metodu, jak převést nadměrné problémy s batohem na běžné problémy s batohem, které k dokončení této změny používají modelové výpočty.

Jak vygenerovat veřejný tajný klíč pomocí soukromého klíče dále: vezměte přírůstkovou sekvenci, například {2, 3, 6, 13, 27, 52}, s n až vezměte všechny položky a pak použijte M k provedení čísel režimů Modul by měl být větší než počet všech čísel v sekvenci, například 105. Násobitel by měl být s libovolným číslem v sekvenci, například 31. obecná sekvence batohu je:

2 * 31 mod105 = 623 * 31 mod105 = 936 * 31 mod105 = 8113 * 31 mod105 = 8827 * 31 mod105 = 10252 * 31 mod105 = 37

Získaný batoh je tedy {62, 93, 81, 88, 102, 37}. Super inkrementální sekvence batohu je soukromý klíč a získaná sekvence batohu je otevřený tajný klíč.

Chcete-li zašifrovat binární zprávu, nejprve ji rozdělte na několik paketů podrobně popsaných v pořadí batohu. Potom se k prezentaci položky použije 1, což znamená, že položka neexistuje, a vypočítá se celková hmotnost batohu. Opakujte tuto operaci pro všechny pakety. Pokud je například zpráva binární číslo 0110001101101101110, je proces šifrování pomocí výše uvedeného algoritmu batohu následující:

Novinky = 011000 110101 10110011000 Korespondence 93 + 81 = 17411010 odpovídá 62 + 93 + 88 + 37 = 280101110 Korespondence = 68 + 801 + 32

Proto je Ciphet 174, 280, 333

Příjemce až po soukromý tajný klíč: Původní super přírůstkový batoh se používá k jeho převedení na hodnotu N a M v běžných batohech. Aby bylo možné zprávu dešifrovat, musí příjemce nejprve vypočítat N ^ {- 1} n-1, aby splnil n * n ^ {- 1} == 1 mod mn * n-1 == 1MODM. Použijte n ^ {- 1} režim N-1 M vynásobte text v hodnotě každé položky a poté jej rozdělte pomocí soukromých batohů.

V tomto příkladu super přírůstkový batoh: {2, 3, 6, 13, 27, 52} m = 105, n = 31, šifrová zpráva je 174, 280, 333. n ^ {- 1} = 61n-1 = 61, takže hodnota šifrového textu musí být vynásobena kostkou 61 105. 174 * 61 MOD 105 = 9 = 3 + 6 korespondence 0111000; 280 * 61 mod 105 = 70 = 2 + 3 + 13 + 52 odpovídá 110101; 333 * 61 mod 105 = 48 = 2 + 6 + 13 + 27 korespondence 0111000; Proto je z následujícího textu na 011000 110101 101110 zřejmé

Vyřešit pouze 6 sekvencí batohu není příliš obtížné, dokonce i stejná sekvence je stejná. Vlastní algoritmus batohu by měl obsahovat alespoň 250 položek. V super inkrementálním batohu je každá hodnota obecně 200 ~ 400. Modul je obecně 100 až 200. Tento algoritmus se používá při skutečném použití s ​​generátorem náhodných sekvencí pro generování těchto hodnot.

U takového batohu je zkoušet využít útok vyčerpáním k jeho rozkladu. I když počítač dokáže vypočítat 1 milionkrát za sekundu, vyzkoušejte všechny možné batůžkáře, 10 ^ {46} 1046.

Protože se říká, že i když nelze dešifrovat použití výfukových útoků, proč je tento algoritmus dokázán nebo prolomen? Některé útraty SHAMIR, algoritmus batohu lze dešifrovat a lze nalézt příslušnou literaturu.