Cipher - Bag алгоритъм за криптографска система с публичен ключ 1

Шифър - Алгоритъм за чанта за криптографска система с публичен ключ 1

Както всички знаем, паролата с публичен ключ, но също така известна като асиметрична парола, е по-често срещана въз основа на следните три математически проблема;

Трудности при декомпозицията на големи фактори (RSA)

Дискретна двойка екстракция (ELGAMAL)

Елиптична крива, дискретна за решаване на проблема от медицинска сестра (ECC)

Това въведение не е горните три вида криптосистеми с публичен ключ, но преди да се появи паролата с публичен ключ, съществува алгоритъмът за шифроване на публична парола, алгоритъмът за раница; алгоритъмът за раница е алгоритъмът за раница, разработен от Merkle и Hellman. Може да се използва само за криптиране и след това ще бъде подобрен от shamir, за да стане достъпен за цифрови подписи;

Безопасността на алгоритъма за раница произхожда от проблем с раница, той е пълен въпрос на NP, но по-късно откри, че алгоритъмът не е безопасен, но тъй като доказва как да използвате NP пълни проблеми за публична парола, струва си изучаване на.

Ето какво представлява алгоритъмът за раница: Описание: даден артикул, всяко тегло е различно, може ли да поставите няколко части в тези артикули в раница, да го направите равно на дадено тегло? Описание на формулата: Дадена е поредица от стойности M1, M2, ..., Mn и S стойност, изчислете BI, удовлетворявайки: s = b1 + b2m2 + ... + bnmns = b1m1 + b2m2 + ... + bnMnbibi стойност Може да бъде 0, 1.1, което показва, че този артикул е в раницата, 0 го означава;

За да дадем прост пример: Тези артикули могат да тежат 1, 5, 6, 11, 14, 20, могат да бъдат сглобени в раница с 5, 6 и 11 и не е възможно раницата да бъде сглобена на 24. Като цяло, времето, необходимо за решаване на този проблем, изглежда експоненциално нараства с увеличаването на броя на елементите;

Идеята на алгоритъма за раницата Merkle-Hellman е да кодира съобщението като решение на проблема с раницата. Дължината на плана е равна на броя на елементите в купчината, а яркият текст съответства на стойността на B, а шифрованият текст се изчислява и стойността се изчислява, а следващата фигура показва абзац от следния пример за криптиране ;

Раницата всъщност съществува в два различни броя:

Линейното време може да бъде решено;

Линейното време не е налично; лесният за решаване проблем с раницата може да бъде модифициран в труден проблем с раницата. Публичният ключ използва труден проблем с раницата, той може лесно да се използва за документиран, но не е възможно да се дешифрира шифрован текст, частните тайни използват лесно за решаване на проблема с раницата, той дава прост метод за дешифриране. Хората, които не знаят дали частните ключове трябва да разбиват шифровани текстове, трябва да решат рядък проблем с раницата.

За лесни решения можете да изберете надценка, тогава съответният проблем с раницата е лесен за решаване. Преодоляваща последователност: Тя е по-голяма от тази на нея, например {1, 3, 6, 13, 27, 52} е суперпоследователност, а {1, 3, 4, 9, 15, 25} не е.

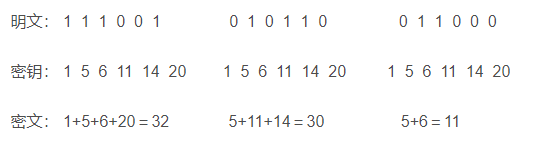
Решението на проблема със свръхинкременталната раница е лесно за намиране, изчислете общото му количество и сравнете максималния брой в последователността, ако общото тегло е по-малко от това число, то не е в раницата, ако общото теглото е по-голямо от това, то е в раницата, раницата Теглото ще бъде извадено, за да се проучи следващото максимално число в последователността, повторете до края. Ако общото тегло е намалено до 0, тогава има само едно решение, в противен случай няма решение.

例如，总重量为70的一个背包，超递增序列为{2，3，6，13，27，52}；最大重量为52，小于70，所以52在背包中，70-52 = 18，下一个重量27 >18，因此，27不在背包中，在下一个13<18，13在背包中，18-13 = 5，以此类推，再下一个，3与2均在背包中，总重量减为0，表明已求出一个解，如果这个一个M-H背包加密分组，那么对应的密文70的解为110101.

Раницата на не-супер-инкременталната последователност е трудна, те нямат бърз алгоритъм. За да решите кой в ​​раницата е да тествате всички решения на свой ред, докато получите правилното решение. Най-бързият алгоритъм все още има затруднения при увеличаване на проблемите в раницата, тъй като последният, когато се присъедините към последователност, решаването трябва само да извърши друга операция.

Алгоритъмът на раницата Merkle-Hellman използва тази природа. Частното ядро ​​е последователност от тежести над проблемите с раница. Публичният ключ е поредица от обикновени проблеми с раница, Merkle и Hellman са проектирали метод за преобразуване на свръхинкрементални проблеми с раница в обикновени проблеми с раница, които използват моделно изчисление, за да завършат тази промяна.

По-нататък как да генерирате публичен таен ключ чрез частен ключ: вземете инкрементална последователност, като {2, 3, 6, 13, 27, 52}, с n до вземете всички елементи и след това използвайте M, за да направите номера на режима Модулът трябва да е по-голям от броя на всички числа в редицата, като например 105. Множителят трябва да бъде с което и да е от числата в редицата, като например 31. Следователно, общата последователност на раницата е:

2 * 31 mod105 = 623 * 31 mod105 = 936 * 31 mod105 = 8113 * 31 mod105 = 8827 * 31 mod105 = 10252 * 31 mod105 = 37

Следователно получената раница е {62, 93, 81, 88, 102, 37}. Супер инкременталната последователност на раницата е частен ключ, а получената последователност на раницата е отворен таен ключ.

За да шифровате двоично съобщение, първо го разделете на няколко пакета, описани подробно в последователността на backpack. След това 1 се използва за представяне на артикула, което показва, че артикулът не съществува, и изчислява общото тегло на раницата. Повторете тази операция за всички пакети. Например, ако съобщението е двоично число 0110001101101101110, процесът на шифроване с помощта на горния алгоритъм за раница е както следва:

Новини = 011000 110101 10110011000 Кореспонденция 93 + 81 = 17411010 съответства на 62 + 93 + 88 + 37 = 280101110 Кореспонденция 62 + 81 + 88 + 102 = 333

Следователно Ciphet е 174, 280, 333

Получателят до частния таен ключ: Оригиналната раница със супер увеличение се използва за преобразуването й в стойността на N и M в общите раници. За да дешифрира съобщението, получателят трябва първо да изчисли N ^ {- 1} n-1, за да отговори на n * n ^ {- 1} == 1 mod mn * n-1 == 1MODM. Използвайте n ^ {- 1} N-1 режим M умножете текст, който струва всеки елемент, и след това използвайте лични раници, за да го разделите.

В този пример, супер инкременталната раница: {2, 3, 6, 13, 27, 52} m = 105, n = 31, шифрованото съобщение е 174, 280, 333. n ^ {- 1} = 61n-1 = 61, така че стойността на шифрования текст трябва да бъде умножена по матрица 61 105. 174 * 61 MOD 105 = 9 = 3 + 6 кореспонденция 0111000; 280 * 61 mod 105 = 70 = 2 + 3 + 13 + 52 съответства на 110101; 333 * 61 mod 105 = 48 = 2 + 6 + 13 + 27 кореспонденция 0111000; Следователно става ясно от следващия текст на 011000 110101 101110

Разрешаването на само 6 последователности от раници не е много трудно, дори една и съща последователност е една и съща. Действителният алгоритъм на раницата трябва да съдържа поне 250 елемента. В супер инкременталната раница всяка стойност обикновено е 200 ~ 400. Модулът обикновено е 100 до 200. Този алгоритъм се използва при реална употреба с генератор на произволна последователност за генериране на тези стойности.

За такава раница опитът да се използва атаката на изтощение, за да се разложи, е безполезен. Дори ако компютърът може да изчисли 1 милион пъти в секунда, опитайте всички възможни туристи, 10 ^ {46} 1046.

След като се казва, че дори ако използването на атаки с изгорели газове не може да бъде дешифрирано, защо този алгоритъм е доказан или кракнат? Някои от разходите на SHAMIR, алгоритъмът на раницата могат да бъдат дешифрирани и може да се намери съответната литература.